Россия
Ангарский государственный технический университет (Вычислительные машины и комплексы, Профессор)
Россия
Приведён анализ метода измерения геометрических размеров объекта на изображении с применением инструментов библиотеки OpenCV
распознавание образов, детектор границ Кэнни, метод, OpenCV
Классификация объектов по сорту может производиться по их геометрическим параметрам, как, например, в случае гранул полистирола. На данный момент подобные операции выполняются «вручную», когда оператор визуально оценивает необходимые в контексте конкретной задачи сортировки геометрические параметры и принимает соответствующее решение.
Однако в ходе работы может сказаться влияние субъективного фактора, что может привести к неверному результату анализа геометрических параметров объекта. В данном случае может понадобиться использование средств автоматизированного распознавания образов, их анализа и принятия соответствующих решений.
Для обнаружения границ и последующего определения контуров объекта на изображении, полученном с камеры, необходимо использование детектора границ, одним из которых является детектор границ Кэнни [1]. Оператор Кэнни (детектор границ Кэнни, алгоритм Кэнни) в области компьютерного зрения – оператор обнаружения границ изображения. Был разработан в 1986 году Джоном Кэнни и использует многоступенчатый алгоритм для обнаружения широкого спектра границ в изображениях.
Кэнни изучил математическую проблему получения фильтра, оптимального по критериям выделения, локализации и минимизации нескольких откликов одного края. Он показал, что искомый фильтр является суммой четырёх экспонент. Он также показал, что этот фильтр может быть хорошо приближен первой производной Гауссианы. Кэнни ввёл понятие подавления немаксимумов, которое означает, что пикселями границ объявляются пиксели, в которых достигается локальный максимум градиента в направлении вектора градиента.
Кэнни обнаружил, что требования к применению краевого детектора в различных системах видеонаблюдения относительно схожи. Решение для обнаружения границ, отвечающее этим требованиям, может быть реализовано в широком диапазоне ситуаций. Общие критерии обнаружения границ включают:
- обнаружение границы с низкой частотой ошибок, что означает, что обнаружение должно точно улавливать как можно больше границ, показанных на изображении,
- точка границы, обнаруженная оператором, должна точно локализоваться в её центре,
- заданная граница на изображении должна быть отмечена только один раз, и, по возможности, шум изображения не должен создавать ложных границ.
Среди разработанных на сегодняшний день методов обнаружения границ алгоритм Кэнни является одним из наиболее строго определенных методов, который обеспечивает хорошее и надежное обнаружение. Благодаря своей оптимальности в соответствии с тремя критериями обнаружения границ и простоте процесса реализации, он стал одним из самых популярных алгоритмов обнаружения границ.
Процесс обнаружения границ алгоритмом Кэнни можно разбить на пять различных этапов:
- применение фильтра Гаусса для сглаживания изображения, чтобы удалить шум,
- нахождение градиентов интенсивности изображения,
- применение порогового значения величины градиента или подавление нижней границы отсечения, чтобы избавиться от ложного отклика на обнаружение границ,
- применение двойной пороговой фильтрации для определения потенциальных границ,
- отслеживание границы с помощью гистерезиса: завершение обнаружения границ путём подавления всех остальных границ, которые являются слабыми и не связаны с сильными границами.
Уравнение Гауссового фильтра для обоих направлений, в которых изменяется градиент изображения, представлено в формуле (1).
(1),
где x и y – расстояния от центра ядра по горизонтали и вертикали соответственно, – стандартное отклонение Гауссового ядра [2].
Гауссово ядро представляет собой матрицу M∙N, где M и N – нечётные положительные числа. Содержимое данной матрицы представляет собой средневзвешенные значения пикселей, где пиксели, наиболее удалённые от центрального, имеют меньший вес в сравнении с расположенными ближе к центру.
В следующей формуле представлено вычисление градиентов изображения, вычисленных с использованием фильтра Собеля:
(2),
где и
– изменение интенсивности изображения центрального пикселя в горизонтальном и вертикальном направлениях соответственно,
– направление, в котором меняется интенсивность градиента.
После получения значений градиентов и изменений интенсивности в обоих направлениях, производится полное сканирование изображения для удаления пикселей, не относящихся к границам. Для этого каждый пиксель проверяется, является ли он локальным максимумом по сравнению с соседними пикселями в заданном направлении вектора градиента. На рисунке 1 представлено графическое представление данного процесса [3].
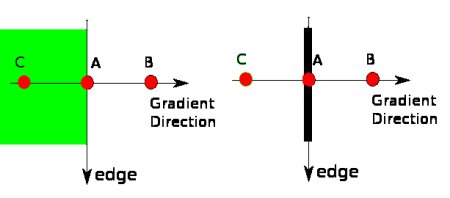
Рисунок 1 – Подавление немаксимумов.
Точка А находится на границе (в вертикальном направлении). Точки B и C находятся на направление градиента. Поэтому точка А проверяется с точками B и C на предмет формирования ими локального максимума. Если они его формируют, то идёт переход к следующему этапу детектирования границ. В противном случае точка А подавляется, то есть, её значение устанавливается в ноль.
На стадии отслеживания границы с помощью гистерезиса происходит проверка, какие из обнаруженных границ являются таковыми, а какие – нет. Для этого берутся два пороговых значения – minVal и maxVal. Любые границы со значением интенсивности градиента выше максимального являются сильными, а те, чьи значения интенсивности ниже минимального, – слабыми и отсекаются в ходе классификации. Границы со значениями, лежащими между минимальным и максимальным, классифицируются на основании их связи с другими границами. Если они связаны с «сильными» пикселями, то считаются частью границ с этими пикселями. В противном случае, они отсекаются. Графическое представление работы данного этапа представлено на рисунке 2.
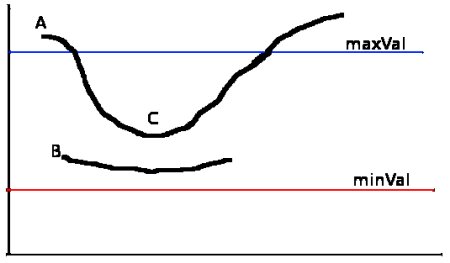
Рисунок 2 – Отслеживание границ с помощью гистерезиса.
Граница А находится выше максимального значения, поэтому считается сильной. Хотя граница С находится ниже максимального, она связана с границей А, поэтому также считается границей. Но граница В, хоть и лежащая выше минимального значения, в том же регионе, что и граница С, не связана с сильной границей, поэтому не проходит выборку.
Также описанная выше стадия убирает небольшие пиксельные шумы на основании того, что границы являются длинными линиями.
Конечный результат работы детектора – сильные границы изображения.
Недостатками метода Кэнни являются:
- фильтр Гаусса, помимо шума, может сгладить высокочастотную характеристику, что увеличит вероятность появления слабых границ,
- метод вычисления амплитуды градиента чувствителен к шумам и может легко обнаруживать ложные границы, теряя при этом реальные,
- детектор использует два фиксированных пороговых значения для фильтрации ложных границ, что может вызывать затруднения с возрастанием сложности изображения,
- результат обнаружения не может обеспечить удовлетворительно высокую точность одного отклика для каждой границы.
Стоит отметить, что существуют способы нивелирования данных недостатков путём применения таких способов, как оператор Щарра, метод Отсу, техника математической морфологии и кёрвлеты.
Измерение размера объекта на изображении схоже с вычислением расстояния от камеры до объекта – в обоих случаях необходимо определить масштаб, измеряемый в «пикселях на заданную метрику» [4]. Перед определением размера объекта необходимо выполнить так называемую «калибровку» с использованием эталонного объекта. Необходимо соблюдение двух следующих условий:
- нужно знать геометрические размеры эталонного объекта, высоту и ширину в измеряемых единицах, таких, как миллиметры, дюймы и так далее,
- нужно иметь возможность найти эталонный объект на изображении, основываясь или на расположении объекта (к примеру, он всегда расположен в левом верхнем углу изображения), или его внешнем виде (выделяющиеся по сравнению с другими объектам на изображении цвет или форма).
В своём примере автор метода в качестве эталонного объекта использует монету номиналом в двадцать пять центов Соединённых Штатов Америки и размещает её в левой части изображения, что позволяет отсортировать контуры слева направо, начиная с монеты, являющейся первым контуром в списке. Далее идёт определение масштаба, измеряемого в «пикселях на метрику». Масштаб представляет собой отношение ширины объекта в пикселях к ширине, измеряемой в заданной метрике. В приводимом примере – в американских дюймах.
Ширина монеты составляет 0,955 дюйма. Предполагая, что в пикселях данная величина будет составлять 150 пикселей, искомая метрика составит 157 пикселей, означая, что на исходном изображении на каждые 157 пикселей будет приходиться 0,955 дюйма.
После определения метрики и определения границ объектов с помощью детектора Кэнни идёт нахождение контуров, соответствующих найденным границам. По нахождению и последующей сортировке контуров они проверяются на предмет того, являются ли они шумами. В положительном случае они отсеиваются.
Далее идёт вычисление и сортировка так называемых «вращающихся ограничивающих прямоугольников» для последующих операций алгоритма. Следующим шагом является вычисление средних точек между верхней левой и верхней правой, между нижней левой и нижней правой, между верхней левой и нижней левой и между верхней правой и нижней правой.
После этого происходит вычисление Евклидовых расстояний между измеренными средними точками. Последним шагом является вычисление размеров объектов путём деления Евклидовых расстояний на ранее измеренную метрику-масштаб.
Стоит отметить, что итоговый результат проведённых измерений может отличаться от реальных. Причины этому автор исходной статьи выделяет две:
1. некорректный угол положения камеры, который должен составлять 90 градусов, в противном случае параметры могут искажаться,
2. отсутствие калибровки самой камеры, без которой так называемые «радиальные и тангенциальные искажения объектива» также могут оказывать влияние на итоговый результат.
Под радиальным искажением понимается тип искажения, обычно возникающий из-за неравномерного преломления света [5]. Лучи больше отклоняются от краев линзы, чем от центра. Из-за радиального искажения прямые линии в реальном мире на изображении кажутся изогнутыми. Луч света смещается в радиальном направлении внутрь или наружу от своего идеального положения, прежде чем попасть на датчик изображения.
Тангенциальное искажение обычно происходит, когда экран или сенсор расположены под углом к объективу. Таким образом, изображение кажется наклоненным и растянутым.
Решение проблемы с калибровкой решается путём вычисления внешних и внутренних параметров. Внешние параметры – это матрицы поворота и перемещения, используемые для преобразования чего-либо из кадра окружающего мира в кадр камеры. Внутренние параметры относятся к самой камере и преобразуют информацию от внешних параметров в пиксель.
Зачастую калибровку камеры выполняют посредством инструментов библиотеки OpenCV, за основу берётся изображение шахматной доски [6]. В качестве преимущества метода с шахматной доской выделяется лёгкость определения образа доски на изображении и углы клеток доски, которые ввиду наличия острых градиентов в двух направлениях и связаны тем, что находятся на пересечении шахматных линий, идеальны для локализации.
1. ResearchGate. A Computational Approach To Edge Detection. – URL: https://www.researchgate.net/publication/224377985_A_Computational_Aproach_To_Edge_Detection (дата обращения 05.04.2025).
2. Pyimagesearch. OpenCV Smoothing and Blurring. 2021. – URL: https://pyimagesearch.com/2021/04/28/opencv-smoothing-and-blurring/ (дата обращения 05.04.2025).
3. OpenCV modules. Canny Edge Detection. – URL: https:// docs.opencv.org/ 4.x/ da/ d22/ tutorial_py_canny.html (дата обращения 05.04.2025).
4. Pyimagesearch. Measuring size of objects in an image with OpenCV. 2021. – URL: https://pyimagesearch.com/2016/03/28/measuring-size-of-objects-in-an-image-with-opencv/ (дата обращения 05.04.2025).
5. LearnOpenCV. Understanding Lens Distortion. 2020. – URL: https://learnopencv.com/understanding-lens-distortion/ (дата обращения 05.04.2025).
6. LearnOpenCV. Camera Calibration using OpenCV. 2020. – URL:https://learnopencv.com/camera-calibration-using-opencv/ (дата обращения 05.04.2025).








